|
|
|
|
|
|
|
|
|
|
Research  |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
| research home | special topics home | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Special Topics | ||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Phase Sensitivity of Bipolar EEG Training Protocols by John A. Putman M.A. M.S. and Siegfried Othmer Ph.D. |
||||||||||||||||||||||||||||||||||||||||||||||||||
John Putman is a Neurofeedback practitioner and researcher at the EEG Institute in Woodland Hills, California with over 12 years experience in the field of biofeedback. Siegfried Othmer is Chief Scientist of the EEG Institute and President of The Brian Othmer Foundation, a non-profit organization for research, education and clinical services in Neurofeedback. He is active as a scientist, teacher, public speaker and writer promoting the understanding and acceptance of Neurofeedback. Introduction All conventional EEG biofeedback to date has been performed with EEG amplifiers with a differential first stage. This is intended to reject extraneous common-mode signals appearing at both active terminals, and has the consequence that common-mode EEG signals are rejected as well. Thus, when bipolar placement is employed clinically, only the activity which differs between the two sites is processed in the down-stream electronics. Thus in-phase, or synchronous, activity is suppressed, and out-of-phase as well as opposite-phase activity is propagated and ultimately rewarded. As a result, the reward waveform is determined primarily by the phase relationship prevailing at the two sites at the center frequency of the reward band. It is also determined by the instantaneous amplitudes at the two sites. It is useful to examine the mathematical particulars in order to make these dependences explicit. These matters are introduced with a vector analysis, and followed with a Monte Carlo calculation of the typical response to be expected in feedback for random inputs. Vector Analysis
For simplicity, consider the amplitudes (A and B) of two vectors (V1 and V2) to be 100uV. The phase angle between the 2 vectors is φ (or "phi"). In the complex plane we have: V1 + V2 = A( e [exp j(wt)] ) +B( e [exp j(wt + φ )] )
= A [cos (wt )+ j sin(wt)] + B[ cos ( wt + φ ) + j sin (wt + φ)]. The sinusoidal dependence is time-invariant (i.e., periodic), so it can be conveniently taken out of the discussion. That is to say, it is only the relative phase that is of interest. (This is the equivalent of talking about the angular separation between two sites on the equator without worrying about the fact that both sites are rotating about the earth's axis.) For simplicity, therefore, it is sufficient to take a snapshot at t = 0. This means that V1 will be assigned a phase of zero degrees. Thus, with wt = 0 and A = B = 100;
where sin (wt) = 0 and cos (wt) = 1 Eq.1 becomes: 100 + 100 [ cos (φ) + j sin (φ)]
Example: for φ = π / 4 (or 45 degrees) V2 = 100 [cos (π/4) + j sin (π/4)]
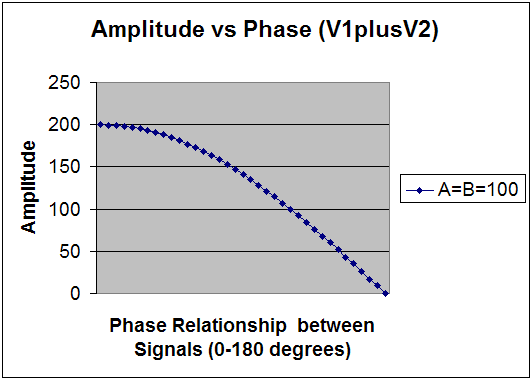
= 70 + j70 thus V1 + V2 = 100 + 70 + j70 where the magnitude of resulting vector (Vr) = 184 and angle of Vr = arcTan (70/170) = π /8 (Note that the angle of Vr is not a phase angle.) For V1+V2 we then have the following relationship between amplitude and phase (Fig.1).
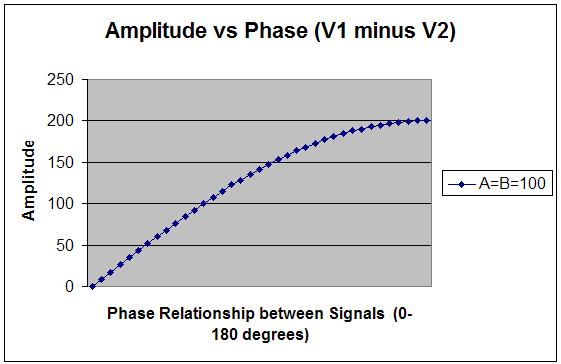
Conversely, in Fig. 2 we have for V1-V2: V1-V2 = 100 - 100[cos (φ) + j sin (φ)];
for φ = π/4 = 100 - 70 - j 70 = 30 -j 70 which implies that Vr =71
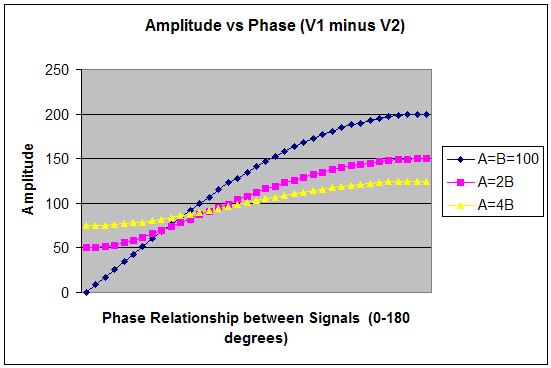
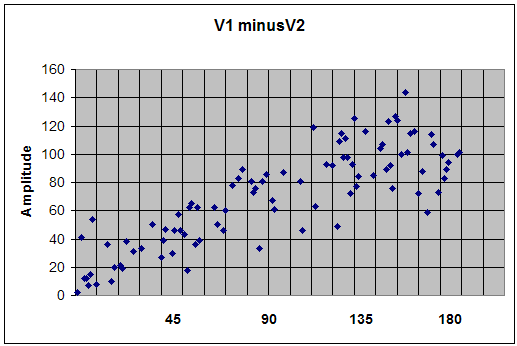
When adding vectors, V1+V2 yields a magnitude that is inversely related to increasing phase angle, as shown in Figure 1. The maximum amplitude is attained at φ = 0 degrees and the minimum at φ = 180 deg. This situation applies when rewarding a frequency in a "sum of channels" mode (with common reference), in which one is effectively encouraging synchrony between the sites. Conversely, when measuring the difference between vectors (V1-V2), the resultant magnitude varies directly with increasing φ where the maximum magnitude is attained at φ = 180 deg and the minimum at φ = 0 deg, as shown in Figure 2. When performing bipolar training, we are concerned only with this relationship. Since the only difference between Figures 1 and 2 lies in the relative phase, it is apparent that bipolar placement serves effectively as a transducer of relative phase into net amplitude. It is, first and foremost, a phase discriminant. The phase dependence is illustrated in Figure 3 for three assumptions of relative amplitudes of V1 and V2. It is apparent that the phase dependence is most determinative in the event that A and B are of comparable amplitude. In cases where there is some amplitude disparity between generators, phase shifts will play a lesser but still significant role in resultant amplitudes. And finally, the case where B is much less than A can be taken to simulate the case of referential placement with ear reference. Relative phase still enters, but may no longer be predominantly determinative for the reward contingencies. (The case B>A represents nothing new because the designations are arbitrary.) In typical trainings, a threshold is selected such that a reward criterion is met for some percentage of the time, e.g. 70%. Whereas the respective amplitudes play into this, the probability of a reward is minimal unless a phase criterion is also met - hence the primacy of phase in training with bipolar placements. A sample Monte Carlo probability analysis illustrates this point for more realistic assumptions. Monte Carlo Calculation
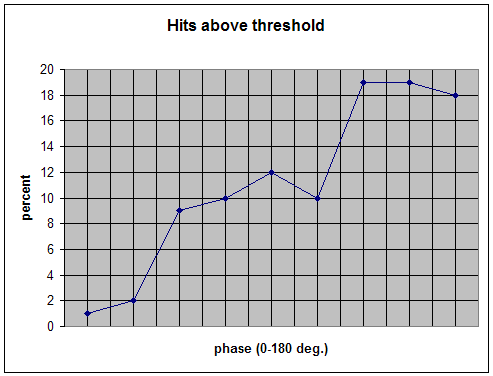
In customary usage a threshold is applied such that a reward issues nominally 70% of the time. Applying that criterion to the "data" of Figure 4 yields a threshold value of 42 on this scale. The resulting distribution of reward probability as a function of phase angle is given in Figure 5. A clear disfavoring of small phase angles is the most prominent feature. Some 97% of hits lie in range of 40-180 degrees in phase angle. Hence the training can be considered one that strongly disfavors phase synchrony.
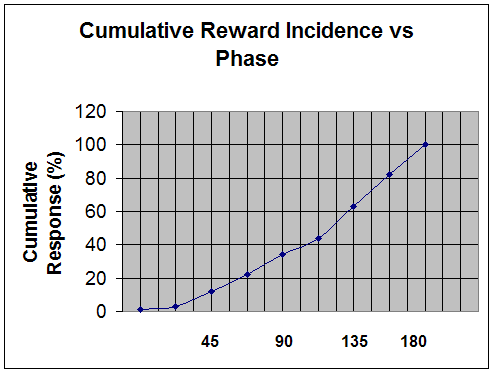
The cumulative distribution derived from the incremental distribution in Figure 5 is shown in Figure 6. This Figure illustrates that only three percent of rewards apply to the case of phase difference less than 40 degrees. With increasingly liberal reward criteria (which are often used), the requisite phase difference will decrease. Thus when performing bipolar training with generous thresholding, the range of phase over which success can be readily achieved is even broader. However, even with a liberal reward scheme we are still encouraging an “anywhere but here” response by the brain (i.e., any phase but synchrony).
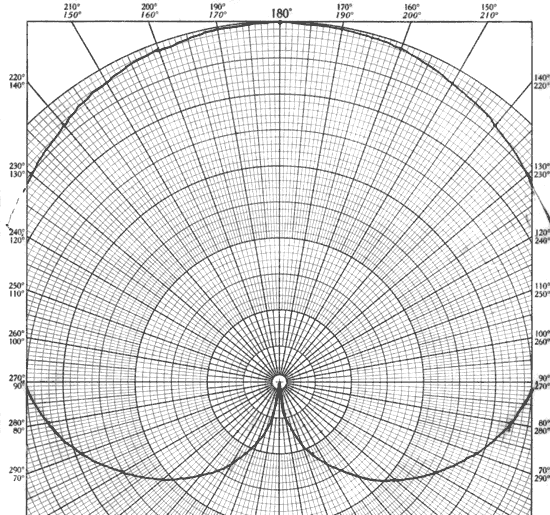
Since inhibits in Neurofeedback amount to nothing more than the withholding of a reward, one could equivalently see the reward-based training in terms of an inhibit on synchronous activity. More specifically, one can consider bipolar training in terms of a "soft inhibit" over a certain range in relative phase, in contrast to the "hard inhibits" we place on amplitudes. Equivalently, one can think of this in terms of an exclusion zone in terms of phase, in this one with soft rather than hard boundaries. This is best illustrated in Figure 7, where Figure 2 has been redrawn as a polar plot. The soft exclusion zone is to be found symmetrically distributed around zero phase angle. It will be observed that the phase dependence of the net signal is very strong within that zone, which motivates our perspective that phase is the driver in bipolar training of the kind being discussed here. Seen in this "inhibit-based" perspective, Figure 7 illustrates the large phase space available for rewards outside of the narrow exclusion zone.
Discussion This treatment is equally applicable to near-neighbor sites, where elevated coherence is expected. Because amplitudes are somewhat correlated between near-neighbor sites, the impact of relative phase on reward incidence is likewise expected to be strong. Hence, bipolar training with near-neighbor placement can also be regarded in terms of promoting desynchronization, as opposed to viewing it in terms of the standard amplitude up-training. Note that the term "desynchronization" is used to describe a condition in which the phase angle is non-zero. This does not necessarily imply anything about coherence. Finally, when excesses in EEG amplitudes are observed at certain frequencies, and reward training with bipolar placement is used in the same EEG band, the result will be a tendency toward desynchronization rather than an exacerbation of the amplitude deviation. In other words, fears about the arbitrary use of this protocol in the face of amplitude elevations are unfounded. Clinical experience is in accord with this. (Othmer, 2005). It is an implicit assumption of this work that training toward desynchronization of the EEG effectively trains down excess coherence. The apparent conflation of these two concepts (synchrony and coherence) is defensible on the basis of findings by Hudspeth that if the phase delay is greater than the equivalent of 10 milliseconds, coherence drops toward insignificance in any event. (Hudspeth, 2000) Thus synchrony is in most instances of clinical import, and at most frequencies employed in EEG training, a viable stalking horse for coherence. At a minimum, the two measures co-vary. It is therefore quite defensible to refer to reward training with bipolar placement in terms of the down-training of coherence. Coherence excesses represent an obvious and common failure mode of the regulation of cortical timing. However, such excesses do not characterize all of the conditions for which interhemispheric training has been found to be helpful. In such cases, one must necessarily think of this training simply as a challenge to the regulatory mechanisms by which interhemispheric timing is organized. Merely the deviation from prevailing states that is evoked through feedback provokes a reaction by the brain in a restorative direction. The repetition of this push-pull dynamic eventuates ultimately in improved regulatory performance. Thus the training may not have to be directed against a particular target of training at all. It may be sufficient simply to mildly challenge the brain out of its prevailing state. And if that is the case, then the distinction between synchrony and coherence is once again a secondary consideration. And if the challenge is non-prescriptive, then it also follows that the clinical benefits should be diagnostically non-specific. Such is the finding. (Othmer, 2005) Summary References
|
||||||||||||||||||||||||||||||||||||||||||||||||||